Share Post:
Mathematics has always been a field that thrives on challenges, pushing human thought to new heights. Some math problems, however, have tested the limits of logic and creativity, remaining unsolved for decades or even centuries.
These difficult math problems are more than intellectual puzzles, they are milestones that have shaped the direction of mathematical research and influenced advancements in:
- Science
- Technology
- Engineering
By examining these historical challenges, one gains insight into how perseverance and innovation have driven humanity’s quest to solve the mysteries of the universe.
Notable Unsolved Problems
Mathematics is a field defined by its challenges, and some math problems stand as towering enigmas that have withstood centuries of effort, like:
- Riemann Hypothesis
- P vs NP Problem
- Navier–Stokes Existence and Smoothness
- Birch and Swinnerton-Dyer Conjecture
- Hodge Conjecture
- Yang-Mills Existence and Mass Gap
These unsolved questions are more than intellectual puzzles. They represent opportunities for progress across science, technology, and theoretical exploration. Therefore, you will frequently find them in high schools and colleges.
By tackling these profound math problems, mathematicians aim to unlock deeper truths about the structures and patterns that govern our world, pushing the boundaries of human knowledge
Riemann Hypothesis
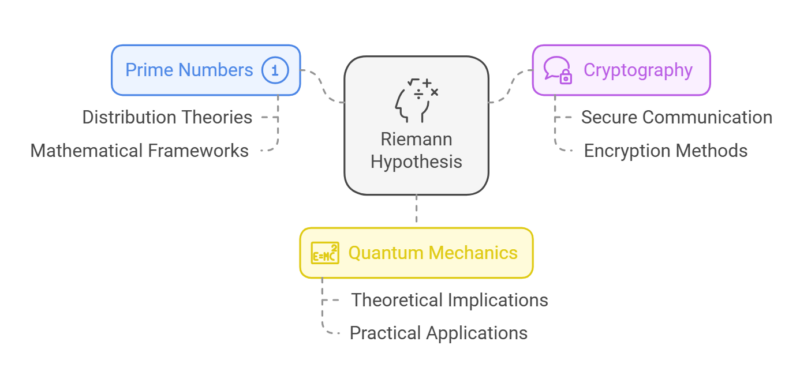
The Riemann Hypothesis addresses the enigmatic relationship between the distribution of prime numbers and the zeros of the Riemann zeta function. Its influence extends across number theory, shaping the foundational understanding of primes, which play a key role in various mathematical frameworks.
- Prime numbers are the building blocks of arithmetic, and insights gained from the hypothesis could reshape theories involving prime distribution.
- Cryptography relies heavily on prime numbers, and advancements in this area could transform secure communication methods.
- In quantum mechanics, connections to the Riemann Hypothesis suggest potential for breakthroughs in the understanding of physical systems.
Despite years of concentrated efforts by mathematicians, the Riemann Hypothesis remains unsolved. Its unsolved status continues to attract some of the brightest minds in mathematics, driving innovations and new methodologies.
P vs NP Problem
P vs NP problem lies at the heart of computational complexity theory. It seeks to determine if every problem whose solution can be verified quickly by a computer can also be solved quickly. Its resolution could redefine computational problem-solving on a global scale.
Implications for Technology:
- Revolutionize algorithm design by making once-intractable math problems solvable.
- Enhance artificial intelligence through new capabilities in data analysis and prediction.
- Overhaul modern cryptographic systems, requiring a reevaluation of data security frameworks.
The P vs NP problem continues to fuel debates and investigations, offering a tantalizing glimpse of how computing could evolve in the future.
Navier–Stokes Existence and Smoothness
The Navier–Stokes equations describe the motion of fluids such as air and water. The problem lies in proving the existence of smooth, well-behaved solutions for all conditions.
Despite its apparent simplicity, this challenge encapsulates a range of unsolved questions in fluid dynamics.
Significance for Science and Engineering:
- Unlock a deeper comprehension of turbulence, which affects weather prediction and climate modeling.
- Advance the design of more efficient transportation and energy systems through refined fluid mechanics.
- Improve simulations in industries such as aviation and automotive engineering.
A solution to this problem would revolutionize the ability to model natural and industrial processes involving fluid motion.
Birch and Swinnerton-Dyer Conjecture
Birch and Swinnerton-Dyer’s conjecture explores the connection between elliptic curves and the number of rational solutions they possess.
Elliptic curves are vital in number theory, underpinning cryptography, and many other mathematical applications.
Applications and Importance:
- Critical for understanding Diophantine equations, which involve solving polynomial equations with integer or rational solutions.
- Provides tools for developing advanced cryptographic protocols.
- Enables better insights into algebraic structures and their properties.
Progress on the Birch and Swinnerton-Dyer Conjecture would open a new frontier in number theory, offering solutions to longstanding questions about rational points on curves.
Hodge Conjecture
The Hodge Conjecture deals with algebraic cycles and their correspondence to cohomology classes in algebraic geometry. Its relevance stretches across geometry and topology, intersecting with fundamental questions about the nature of spaces and shapes.
Impact:
- Enhances the study of algebraic varieties, which are central objects in algebraic geometry.
- Provides insights into the topology of higher-dimensional spaces.
- Influences theoretical physics, particularly in string theory and quantum field theory.
Resolving this conjecture would create new avenues for theoretical exploration and broaden the scope of research in geometry and topology.
Yang-Mills Existence and Mass Gap
The Yang-Mills problem focuses on the mathematical properties of quantum field theory. Specifically, it addresses the existence of solutions to the Yang-Mills equations that exhibit a mass gap, a phenomenon observed in particle physics.
Relevance to Physics and Mathematics:
- Provides a foundation for understanding fundamental forces such as the strong nuclear force.
- Bridges gaps between mathematics and particle physics, offering insights into quantum phenomena.
- Strengthens the mathematical models used in quantum field theory, leading to potential advancements in applied physics.
A solution to the Yang-Mills problem would deepen the connection between abstract mathematics and the physical world, enhancing our grasp of the universe’s underlying principles.
Historical Context
Throughout history, challenging mathematical problems have played a crucial role in advancing the field by setting benchmarks for research and sparking innovation.
Two monumental compilations, Hilbert’s Problems, and the Millennium Prize Problems, have significantly shaped the course of mathematical progress.
While separated by a century, these collections share a common goal: to challenge humanity’s intellectual capabilities and fuel breakthroughs in mathematical thinking.
Hilbert’s Problems
In 1900, David Hilbert introduced a collection of 23 math problems at the International Congress of Mathematicians in Paris.
This groundbreaking initiative defined many of the major research goals for the 20th century and shaped how mathematicians approached the discipline.
His problems spanned numerous areas, including geometry, number theory, and logic, and offered a sense of direction for mathematicians worldwide.
Key highlights of Hilbert’s Problems:
- The problems covered a broad spectrum, including foundational issues in set theory and physics.
- While several problems were solved, others remain open, continuing to drive research in modern mathematics.
- Hilbert’s initiative fostered an era of international cooperation among mathematicians, setting a precedent for shared intellectual challenges.
For example, although Fermat’s Last Theorem was not one of Hilbert’s original 23 problems, its eventual resolution in the 1990s relied on techniques and methods inspired by questions closely tied to Hilbert’s vision. This reflects the interconnected nature of mathematical challenges and their solutions.
Millennium Prize Problems
In 2000, the Clay Mathematics Institute introduced the Millennium Prize Problems, a set of seven unsolved mathematical questions.
Each problem came with a $1 million reward for a correct solution, symbolizing the immense importance of these challenges to contemporary mathematical research.
While the financial incentive drew attention, it is the intellectual challenge that continues to inspire mathematicians worldwide.
Key aspects of the Millennium Prize Problems:
- Critical Areas of Focus: The problems include topics such as:
- Computational complexity (e.g., the P vs NP problem)
- Fluid dynamics (Navier–Stokes equations)
- Quantum field theory (Yang–Mills Existence and Mass Gap)
- Interdisciplinary Impact: Solutions to these math problems could influence fields as diverse as computer science, physics, and cryptography.
- Guidance for Modern Research: By identifying these problems, the Clay Institute set the agenda for significant mathematical breakthroughs in the 21st century.
Although no mathematician has solved the majority of these questions, their influence on research priorities remains undeniable. Grigori Perelman’s proof of the Poincaré Conjecture is a prime example of how tackling these problems can revolutionize entire fields of study.
While Perelman famously declined the monetary reward, his work has had a lasting influence on topology and geometry.
Impact of Solving These Problems
Solving the most challenging math problems has always been a catalyst for advancing science, technology, and human thought.
These problems are not isolated puzzles; they are central to understanding complex systems and phenomena across multiple disciplines.
Each solution unlocks new possibilities, reshapes foundational knowledge, and has the potential to transform industries.
Their impact extends far beyond academia, influencing everyday life and inspiring generations of researchers.
Advancements in Theory and Practice
The resolution of math problems often leads to groundbreaking theoretical innovations, enhancing the way we approach complex systems and phenomena. For example:
- Improved Mathematical Frameworks: Solved problems often result in the development of entirely new mathematical tools and theories, benefiting various fields.
- Cross-Disciplinary Applications: Insights gained frequently extend into physics, computer science, economics, and engineering.
Practical Applications
These problems often have real-world implications, enabling technological progress and addressing societal challenges. Key areas of impact include:
- Solutions like those for the Navier–Stokes equations could revolutionize fluid dynamics, improving weather prediction, transportation, and energy efficiency.
- Addressing the P vs NP problem could redefine computational efficiency and transform cybersecurity.
- Advances in number theory, such as progress on the Riemann Hypothesis or Birch and Swinnerton-Dyer Conjecture, directly enhance encryption techniques.
Inspiring Future Generations
The pursuit and eventual resolution of these problems inspire curiosity and dedication in mathematicians. They also serve as a benchmark for future research:
- These problems motivate students to engage with higher-level mathematics, fostering a deeper interest in problem-solving.
- Eforts to solve these questions unite researchers across nations, creating a spirit of shared intellectual pursuit.
Broader Influence on Science and Technology
Finally, breakthroughs in solving these problems often ripple outward, affecting related domains and shaping the direction of innovation:
- Mathematical discoveries lay the groundwork for advancements in artificial intelligence, quantum computing, and other cutting-edge technologies.
- The process of tackling such problems encourages systematic, creative, and critical thinking, benefiting multiple disciplines.
These problems represent not just challenges but opportunities to push the boundaries of knowledge and achieve progress that impacts both theory and application.
The Bottom Line
The most challenging math problems in history symbolize humanity’s drive to confront the unknown and unravel the complexities of our universe. These puzzles not only test the limits of intellectual ingenuity but also pave the way for advancements that shape science, technology, and countless other fields.
Each unresolved question holds the potential to unlock profound insights, fostering progress and innovation.
The pursuit of solutions reflects an enduring commitment to discovery, inspiring future generations to continue pushing the boundaries of knowledge.
