Arithmetic vs. Geometric Sequences – Key Differences Explained

Arithmetic is all about numbers and the things we do with them, like adding, subtracting, multiplying, and dividing.

It’s like the math version of solving puzzles to find a single, clear answer. The word “arithmetic” comes from a Greek word, “arithmos,” which means “numbers.”

Cool, right? It’s a special part of math where we learn how numbers work and play together!

Now, let’s talk about sequences. Imagine a line of numbers arranged in a special order.

That’s what a sequence is! There are two really popular types: arithmetic sequences and geometric sequences. In an arithmetic sequence, the numbers change by adding or subtracting the same amount every time—like counting by 2s (2, 4, 6, 8).

In a geometric sequence, the numbers grow (or shrink) by multiplying or dividing by the same number each time—like doubling (2, 4, 8, 16). It’s like numbers following their own little rules!

Arithmetic Sequence

An Arithmetic Sequence is a list of numbers where the difference between any two consecutive terms is always the same. It is based on natural numbers, which are the building blocks of counting and basic arithmetic operations. Think of it like stepping up a staircase, where each step is the same height! The next number in the sequence is found by adding (or subtracting) a fixed number to the one before it.

Here’s what an Arithmetic Sequence looks like:
a, a + d, a + 2d, a + 3d, a + 4d…

• a = the first number in the sequence
• d = the difference added to each term to get the next

For example:
5, 11, 17, 23, 29, 35, …
Here, the difference (d) is 6, because each number is 6 more than the one before it.

Geometric Sequence

Here’s what a Geometric Sequence looks like:
a, ar, ar², ar³, ar⁴…

• a = the first number in the sequence
• r = the ratio or multiplier

For example:
2, 6, 18, 54, 162, …
Here, the multiplier (r) is 3, because each number is 3 times bigger than the one before it.

How to Differentiate Between Them

Are your students learning about arithmetic and geometric sequences? Try out this @openmiddle problem from @Math_m_Addicts with them. https://t.co/nem2EgyliA #MTBoS pic.twitter.com/wY6V8IYziA

— Robert Kaplinsky (@robertkaplinsky) March 14, 2024

• Arithmetic Sequence: Each term is found by adding or subtracting a fixed value (common difference, d).
• Geometric Sequence: Each term is found by multiplying or dividing by a fixed value (common ratio, r).
• Arithmetic sequences change linearly, while geometric sequences grow or shrink exponentially.
• Infinite arithmetic sequences always diverge, while infinite geometric sequences can either converge or diverge.

Examples

What is a Geometric Sequence, and why is it called that?

A geometric sequence is a series of numbers where each term is found by multiplying or dividing the previous term by a fixed value. It’s called geometric because of this consistent ratio.

Can a sequence be both Arithmetic and Geometric?

No, a sequence cannot be both. Arithmetic sequences have a constant difference between terms, while geometric sequences have a constant ratio. These two properties are mutually exclusive.

What is ‘a’ in an Arithmetic Sequence?

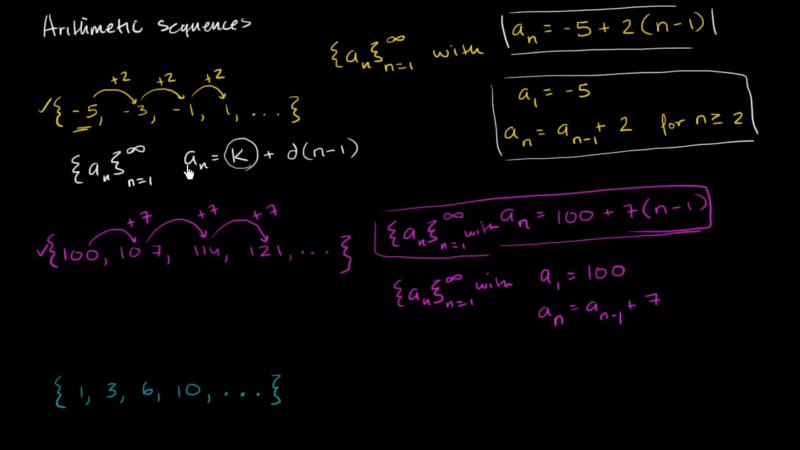
In an arithmetic sequence, ‘a’ represents the first term in the series.

How do you find the nth term of an Arithmetic Sequence?

The nth term of an arithmetic sequence can be calculated using the formula:
an = a + (n − 1) d
Where:

• a = the first term
• d = the common difference

How do you find the nth term of a Geometric Sequence?

The nth term of a geometric sequence can be calculated using the formula:
an = arⁿ⁻¹
Where:

• a = the first term
• r = the common ratio