Share Post:
A point is a fundamental concept in geometry. It represents an exact location in space. Points have no size, length, width, or depth. They serve as the building blocks for more complex geometric shapes and structures.
This article will explain what a point is, its properties, and its importance.
Table of Contents
ToggleDefinition of a Point
A point has no dimensions—no length, width, or height. It is often represented by a dot and named with a capital letter, like A or B. Despite its simplicity, the point is a building block for all geometric shapes and structures.

Key Properties
- No Dimensions: It does not have a size or shape. It is purely a position.
- Representation: They are usually represented as dots on diagrams and are labeled with capital letters.
- Fundamental Element: They are used to define lines, planes, and other geometric figures.
Types of Points
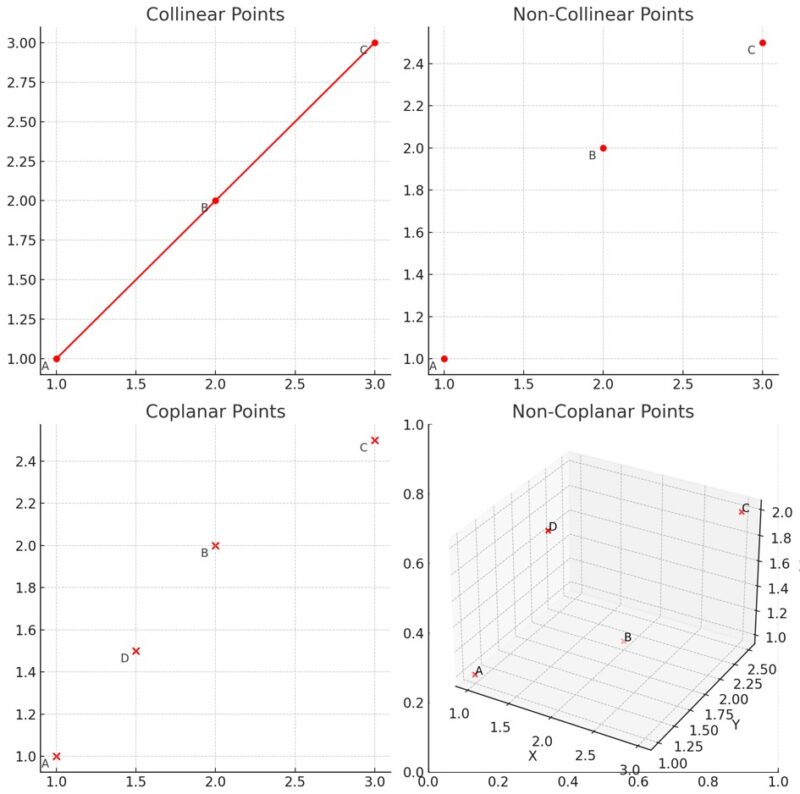
- Collinear Points: Lie on the same straight line.
- Non-Collinear Points: Do not lie on the same line.
- Coplanar Points: Lie on the same plane.
- Non-Coplanar Points: Do not lie on the same plane.
Points in Cartesian Coordinates
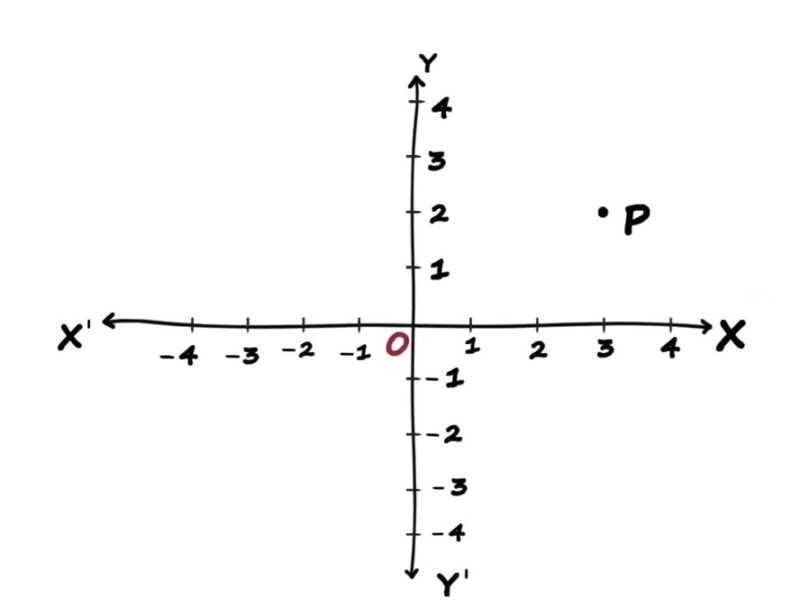
In a Cartesian coordinate system, a point’s position is described using coordinates. In two dimensions, a point is represented as (x, y). In three dimensions, it is represented as (x, y, z).
Examples
- Map Locations: Points are used to mark specific locations on maps.
- Graphing: Points represent data values in graphs.
Also, learn more about BODMAS, BIDMAS, and PEMDAS.
Properties
Points have distinct characteristics that make them fundamental in geometry. They are zero-dimensional, meaning they have no length, width, or depth. This lack of dimensions distinguishes them from other geometric entities.
Characteristics
- Zero Dimensions: They occupy no physical space.
- Positional: They specify an exact location.
- Labeling: Typically denoted by capital letters.
Use
- Defining Shapes: Serve as the vertices of polygons.
- Coordinate Systems: Used to describe positions in systems like Cartesian coordinates.
Types
| Collinear | Lie on the same straight line. |
| Non-Collinear | Do not share the same line. |
| Coplanar | Lie on the same plane. |
| Non-Coplanar | Do not share the same plane. |
Points in Euclidean Geometry
In Euclidean geometry, a point is an essential and basic concept. Defined by the ancient mathematician Euclid as “that which has no part,” a point marks an exact location in space. Points have no dimensions—they do not have length, width, or height.
Key Concepts
- Primitive Notion: A point is considered a primitive notion in Euclidean geometry, meaning it is an undefined term that forms the foundation for other definitions and concepts.
- Indivisibility: Points are indivisible and cannot be broken down into smaller components. They are purely positional.
- Role in Geometry: Points are used to define lines, angles, and shapes. For example, a line is formed by connecting two points, and shapes are defined by the vertices, which are points.
Practical Application
Points are used in various geometric constructions and proofs. They are critical in defining the structure of geometric objects and understanding spatial relationships and properties. In more advanced geometry, points play a key role in logical reasoning and proof writing. One such method is the Two-Column Proof, which helps structure geometric arguments step by step.
Points in Cartesian Coordinates
In the Cartesian coordinate system, points are used to specify locations on a plane or in space. Each point is identified by a set of coordinates, which indicate its exact position relative to a reference origin.
Key Concepts
- Two-Dimensional Coordinates: In a 2D plane, a point is represented by an ordered pair (x, y). The x-coordinate shows the position along the horizontal axis, while the y-coordinate shows the position along the vertical axis.
- Three-Dimensional Coordinates: In 3D space, a point is represented by an ordered triplet (x, y, z). The z-coordinate adds depth to the location, indicating its position along the third axis.
Importance in Geometry
Understanding the concept of a point is crucial in the study of geometry. Points serve as the foundation for constructing and defining all other geometric shapes and structures.
Building Blocks
Points are the basic units from which lines, shapes, and solids are constructed. By connecting two points, a line segment is formed. Multiple line segments connected together create polygons and other shapes.
Defining Shapes
Geometric shapes are defined by their vertices, which are specific points. For instance, a triangle has three vertices, each representing a point. Similarly, more complex shapes like polygons and polyhedra are composed of multiple vertices.
Spatial Relationships
Points help in understanding spatial relationships and properties. They define the location and arrangement of shapes in a given space, making it possible to study and analyze geometric figures.
FAQs
What is the difference between a point and a line?
A point represents an exact location in space with no dimensions, while a line is a one-dimensional object that extends infinitely in both directions, defined by connecting two points.
How are points used in computer graphics?
In computer graphics, points are used as reference markers to create and manipulate shapes, models, and animations. They help define vertices of polygons and control the positioning of objects.
Can points be used to measure distances?
Yes, points can be used to measure distances. The distance between two points can be calculated using the distance formula, which is derived from the Pythagorean theorem.
How do points help in navigation systems?
In navigation systems, points are used as waypoints to mark specific locations. These points help in plotting routes and guiding users to their destinations.
Are there any special types of points in geometry?
Yes, there are special types of points such as the centroid, which is the center of mass of a shape, and the circumcenter, which is the center of the circle passing through all vertices of a polygon.
Conclusion
Points are the most basic elements in geometry, serving as the foundation for all geometric shapes and structures. They represent exact locations in space without dimensions. Understanding points is essential for grasping more complex geometric concepts and their practical applications.
From defining lines and shapes to their use in navigation systems and computer graphics, points play a crucial role in both theoretical and applied geometry.
Related Posts:
- Natural Numbers - Definition, Properties, and Examples
- What Are Irrational Numbers - Definition, Examples &…
- Whole Numbers Explained - Definition, Uses, and Key…
- How to Write a Two Column Proof in Geometry?
- What Are the Types of Polynomials? Definitions and Examples
- Complete Guide to Teaching Math with Base 10 Blocks…