Share Post:
From the intricate geometric designs of ancient Egypt to the complex algorithms that drive today’s digital world, mathematics has shaped civilizations, underpinned discoveries, and made sense of the universe. But who can we credit for inventing mathematics?
Mathematics didn’t just appear out of nowhere; it evolved over centuries, varying among different cultures and epochs.ย The origins of mathematics are a subject of ongoing research and debate.
Early human societies recognized the necessity of basic arithmetic and geometric principles for survival – for trading, land measurement, architecture, and astronomical observation. But pinning down the precise time and place of the inception of mathematics remains elusive.
Pioneers of Arithmetic and Geometry
The Dawn of Arithmetic
Historically, the earliest evidence of mathematical knowledge dates back to the ancient Sumerians of Mesopotamia around 4,000 BCE. Sumerians used a sexagesimal (base-60) number system, which is the foundation for the way we measure time today.
Sumerians developed this number system to facilitate trade, land division, and taxation. They inscribed these mathematical concepts on clay tablets, giving us a glimpse into the origins of arithmetic.
Geometry in Land Measurement
In addition to arithmetic, the Sumerians also demonstrated an understanding of basic geometry, primarily for practical applications such as land measurement. Land was a crucial resource for agriculture, so accurate measurement was vital.
Geometric principles enabled the Sumerians to measure fields and divide land accurately. The ancient clay tablets reveal their knowledge of squares, rectangles, and triangles, illustrating the first recorded use of geometry.
Egyptian Mathematics
Building Pyramids: A Geometric Feat
The ancient Egyptians took mathematical principles a step further. Around 2700 BCE, they built the Step Pyramid, showcasing their command over advanced geometric principles. Their ability to construct such monumental structures testifies to their mathematical prowess.
The Pyramids, particularly the Great Pyramid of Giza, display an amazing degree of precision in design and alignment, which couldn’t have been achieved without substantial mathematical knowledge. The Egyptians used their understanding of mathematics not only for practical purposes but also to create harmony with the universe.
Hieroglyphics and Egyptian Numerals
Egyptian numerals were based on a decimal system, which is a stark contrast to the Sumerian sexagesimal system. They used hieroglyphics to denote numbers and mathematical operations. The numeral system used by the Egyptians was additive, meaning the value of the number was the sum of the symbols.
Here’s a snapshot of the ancient Egyptian numeral system:
| Hieroglyphic | Value |
|---|---|
| Single Stroke | 1 |
| Arch | 10 |
| Spiral | 100 |
| Lotus Plant | 1,000 |
| Finger | 10,000 |
| Tadpole | 100,000 |
| Man/Woman | 1,000,000 |
The Greeks
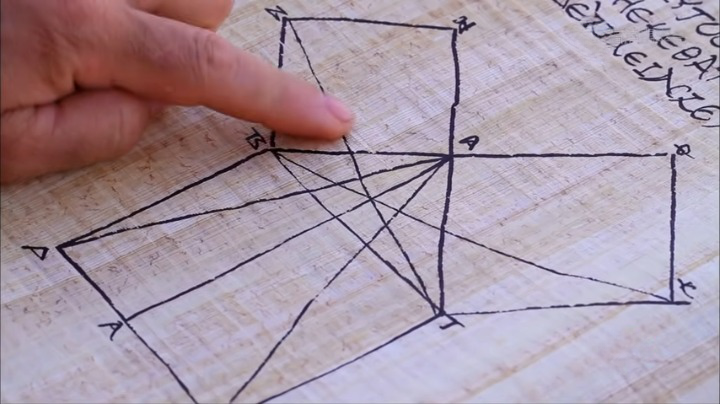
Pythagoras and the Birth of Theoretical Math
The Greek mathematician Pythagoras, born around 570 BCE, is often associated with the beginnings of theoretical mathematics. Pythagoras and his followers, the Pythagoreans, delved into abstract mathematical concepts independent of their practical applications.
The Pythagorean theorem, the proposition that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides, is attributed to Pythagoras.
This theorem is one of the cornerstones of geometry, and its discovery signifies a key shift toward theoretical mathematics.
Euclid and the Foundation of Geometry
Around 300 BCE, Euclid, another Greek mathematician, brought systematic rigor to geometry, culminating in his masterpiece, “Elements”. This work, which comprises 13 books, is the earliest comprehensive treatise on mathematics and has informed the study of geometry for over two millennia.
Euclid’s “Elements” embodies the axiomatic method, a technique that has become the foundation of modern mathematics. This method involves starting with a set of self-evident truths (axioms) and deriving complex theorems from them.
Euclid’s work, therefore, not only contributed to geometry but also paved the way for future mathematical logic.
Zero, Infinity, and Decimal System
The Inception of Zero
The concept of zero, which is fundamental to mathematics, originated in India around the 5th century. The Indian mathematician Brahmagupta was among the first to provide rules involving zero, treating it as a number in its own right.
Before the introduction of zero, there was no placeholder in the numeral system, making calculations with large numbers cumbersome. The innovation of zero dramatically transformed arithmetic and algebra, rendering computations more efficient.
Decimal System and Infinity
Another revolutionary contribution by Indian mathematicians was the decimal system, including the use of place value, around the 6th century. This system, which we still use today, made calculations simpler and more accurate.
Indian mathematicians also grappled with the concept of infinity, acknowledging it as a number that’s larger than any other number. Infinity became instrumental in the development of calculus centuries later.
Chinese Mathematics
Magic Squares and Combinatorics
Chinese mathematics, dating back to 1100 BCE, was marked by an interest in numbers and their properties. The “Lo Shu Square” or the Magic Square of order three was an early example of their fascination with numbers. In a Magic Square, the sums of numbers in all rows, columns, and diagonals are equal.
The ancient Chinese also delved into combinatorics, the study of counting and arranging objects. Their understanding of permutations and combinations greatly influenced the development of this field.
Algebraic Equations and The Nine Chapters
The “Nine Chapters on the Mathematical Art”, an influential Chinese mathematical text from around 200 BCE, explored methods for solving linear and quadratic equations, showcasing an advanced understanding of algebra.
This work, which blended practical and theoretical mathematics, illustrates the breadth of Chinese mathematical thought.
Islamic Golden Age
During the Islamic Golden Age (8th to 14th century), scholars made considerable efforts to preserve Greek mathematical works, which were at risk of being lost. They translated these works into Arabic, ensuring that the mathematical knowledge of the Greeks was passed on to subsequent generations.
Muslim scholars did not just preserve the knowledge, but they also critiqued and expanded upon the Greek mathematical heritage. This era was marked by significant advancements in algebra, geometry, and arithmetic.
Algebra and Algorithms (Contributions by Al-Khwarizmi)
The Persian mathematician Al-Khwarizmi, living in the 9th century, is credited with significant contributions to algebra. His book “The Compendious Book on Calculation by Completion and Balancing” laid down systematic rules for solving linear and quadratic equations.
Al-Khwarizmi’s name also gave us the term “algorithm”, a step-by-step procedure for calculations. Algorithms form the backbone of modern-day computer science, underscoring the enduring influence of Al-Khwarizmi’s work.
Why Was Math Invented?
Mathematics didnโt just appear out of nowhereโit grew out of necessity. From the earliest days of human existence, people faced practical problems that called for creative solutions, and math became the ultimate problem-solving tool.
Think about agriculture. Early farmers needed to track seasons, plan planting schedules, and measure their harvests. Mathematics made it possible to organize this vital work. Geometry came into play when communities began designing homes and later constructing temples, pyramids, and other architectural marvels.
Math wasnโt confined to the ground, though. Ancient civilizations looked up at the stars, using math to decode the mysteries of the sky. Astronomy relied on mathematical principles for charting celestial movements, which also helped improve navigation. Navigational excellence wasnโt just for explorers; it was essential for trade, connecting distant cultures through oceans and deserts.
Economics, too, owes a huge debt to math. Counting goods, balancing resources, and developing early forms of currency required number systems that could handle the complexity of growing societies. Engineering and technology followed, driven by the need for precision and innovation in everything from building aqueducts to designing the tools of the industrial age.
Modern Math
Mathematics has come a long way from tally marks on cave walls to the intricate systems we rely on today. Modern math is more than equations and numbers; itโs a living, evolving language that connects the dots in countless areas of life. From designing algorithms that power the internet to predicting weather patterns, the applications are as vast as they are fascinating.
Terms like diophantine equations, Lie theory, and functional analysis may sound intimidating, but theyโre essential building blocks for solving real-world problems. Fields like chaos theory and fractal geometry have given us tools to model phenomena as diverse as stock market trends and the growth of plants. Meanwhile, game theory finds its way into everything from economics to evolutionary biology, proving that math isnโt just for textbooksโitโs a driving force in decision-making.
The rise of big data has turned computational mathematics into a cornerstone of technology. Think of personalized recommendations on streaming platforms or self-driving cars; none of it would be possible without the algorithms behind the scenes. Similarly, topology and mathematical logic are the unsung heroes in fields like robotics and artificial intelligence.
What makes modern math even more exciting is how it encourages collaboration. Interdisciplinary research brings mathematicians together with scientists, engineers, and even artists to tackle challenges and create solutions that wouldnโt be possible in isolation. The shift toward symbolism and notation has also made concepts more accessible, enabling faster progress and clearer communication across disciplines.
Most Influential Mathematicians
The field of mathematics has been shaped by many brilliant minds from various cultures and eras, each contributing to our collective understanding of the universe. There are countless mathematicians who have made significant contributions to this field throughout history. Here are some of the most famous and significant ones:
| Mathematician | Nationality | Known For |
|---|---|---|
| Euclid | Greek | “Father of Geometry”, author of “Elements” |
| Pythagoras | Greek | Pythagorean theorem in Euclidean geometry |
| Archimedes | Greek | Contributions to the understanding of the principles of lever and buoyancy |
| Isaac Newton | English | Laws of motion and universal gravitation, development of calculus |
| Carl Friedrich Gauss | German | Contributions to number theory, algebra, statistics, analysis, differential geometry, geodesy, geophysics, mechanics, electrostatics, astronomy, matrix theory, and optics |
| Leonhard Euler | Swiss | Contributions to infinitesimal calculus and graph theory, introduced modern mathematical terminology and notation |
| Bernhard Riemann | German | Contributions to analysis, number theory, and differential geometry, including the Riemann integral |
| John von Neumann | Hungarian-American | Major contributions to mathematics, physics, economics, computing, and statistics |
| Alan Turing | English | Considered the father of theoretical computer science and artificial intelligence |
| Andrew Wiles | English | Known for proving Fermat’s Last Theorem |
The Philosophical Roots of Numbers and Ideas
Have you ever paused to think about how abstract numbers and mathematical ideas came to be? The journey from raw observation to deep, abstract concepts is more fascinating than many realize. Mathematics, at its core, isn’t just about crunching numbersโit’s about shaping how we think, reason, and connect with the world around us.
Philosophers like Plato believed in the existence of perfect mathematical formsโabstract entities that could only be grasped by the mind. Concepts like zero, infinity, and negative numbers might feel routine now, but their arrival shook the intellectual world. They forced thinkers to stretch their imaginations and redefine the boundaries of logic and meaning.
From group theory and category theory to metric and topological spaces, math has evolved as a playground for abstract thought. Axioms form its backbone, laying the groundwork for everything from simple addition to the complexities of abstract algebra. The process isnโt just about solving problems but building frameworks that change how we see reality.
FAQs:
Conclusion
To sum up, mathematics is not the invention of a single civilization or individual; it’s the collective achievement of humanity over thousands of years.
Just as our ancestors used mathematics to measure lands, build pyramids, and understand the universe, we use it today to analyze complex data, create secure communications, and even model the behavior of black holes.
Mathematics, as an ongoing human endeavor, remains at the heart of our quest to understand and navigate the world around us. From ancient civilizations to today’s digital world, mathematics continues to shape our lives, our technologies, and our understanding of the universe.
The story of mathematics is far from over, and we look forward to seeing where it takes us next!
